problemas de movimiento angular
Sección 6.1 Segunda Ley de Newton aplicada al Movimiento Circular Uniforme
Problema 6.1 Edición quinta; Problema 6.1 Edición cuarta SERWAY
Un carro de juguete que se mueve con rapidez constante completa una vuelta alrededor de una pista circular (una distancia de 200 metros) en 25 seg.
a) Cual es la rapidez promedio?
b) Si la masa del auto es de 1,5 kg. Cual es la magnitud de la fuerza central que lo mantiene en un circulo?
a) Cual es la rapidez promedio?
b) Si la masa del auto es de 1,5 kg. Cual es la magnitud de la fuerza central que lo mantiene en un circulo? L = 200 metros = 2 π r
Despejamos el radio

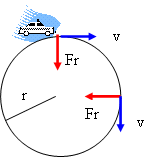
F = 3,01 Newton
Problema 6.2 Edición cuarta SERWAY; Problema 6.5 Edición quinta;
En un ciclotrón (un tipo acelerador de partículas), un deuterón (de masa atómica 2u ) alcanza una velocidad final de 10 % de la velocidad de la luz, mientras se mueve en una trayectoria circular de 0,48 metros de radio. El deuterón se mantiene en la trayectoria circular por medio de una fuerza magnética. Que magnitud de la fuerza se requiere?
Velocidad de la luz = 3 X 108 m/seg
Velocidad del deuterón = 3 X 107 m/seg
Masa deuterón 2u = 2 * 1,661 X 10-27 kg.
Masa deuterón 2u = 3,322 X 10-27 kg.

Problema 6.2 Edición quinta SERWAY
Una patinadora de hielo de 55 kg se mueve a 4 m/seg.. Cuando agarra el extremo suelto de una cuerda, el extremo opuesto esta amarrado a un poste.
Después se mueve en un circulo de 0,8 m de radio alrededor del poste.
a) Determine la fuerza ejercida por la cuerda sobre sus brazos.
b) Compare esta fuerza con su peso.
- Determine la fuerza ejercida por la cuerda sobre sus brazos.
T = 1100 Newton
b) Compare esta fuerza con su peso.
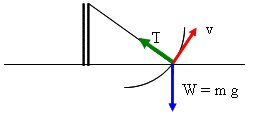
Problema 6.3 Edición quinta SERWAY
Una cuerda ligera puede soportar una carga estacionaria colgada de 25 kg. antes de romperse. Una masa de 3 kg unida a la cuerda gira en una mesa horizontal sin fricción en un circulo de 0,8 metros de radio. Cual es el rango de rapidez que puede adquirir la masa antes de romper la cuerda?
La cuerda se rompe cuando se le cuelgue una masa de 25 kg. Entonces podemos calcular la máxima tensión que soporta la cuerda antes de romperse.
TMAXIMA = m * g = 25 kg * 9,8 m/seg2 = 245 Newton.
Con la tensión máxima que soporta la cuerda antes de romperse, se calcula la máxima velocidad que puede girar la masa de 3 kg antes de romper la cuerda.
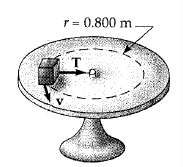
Despejando v
v < 8,08 m/seg. La velocidad de la masa de 3 kg, no puede alcanzar la velocidad de 8,08 m/seg por que se rompe la cuerda.
Problema 6.4 Edición quinta; Problema 6.35 Edición cuarta SERWAY
En el modelo de Bohr del átomo de hidrogeno, la rapidez del electrón es aproximadamente 2,2 * 106 m/seg. Encuentre:
a) La fuerza que actúa sobre el electrón cuando este gira en una orbita circular de 0,53 * 10- 10 metros de radio
b) la aceleración centrípeta del electrón.
Masa = 9,11 * 10- 31 Kg. V = 2,2 * 106 m/seg. r = 0,53 * 10- 10 metros


F = 83,192 * 10- 9 Newton
b) la aceleración centrípeta del electrón.

a = 9,132 * 1022 m/seg2
Problema 6.6 Edición quinta SERWAY. Problema 6.6 Edición cuarta SERWAY
Un satélite de 300 kg. de masa se encuentra en una orbita circular alrededor de la tierra a una altitud igual al radio medio de la tierra (Véase el ejemplo 6.6). Encuentre:
a) La rapidez orbital del satélite
b) El periodo de su revolución
c) La fuerza gravitacional que actúa sobre el?
Datos: RE = radio de la tierra = 6,37 * 106 metros.
h = La distancia entre el satélite y la superficie de la tierra, en este problema es igual a RE
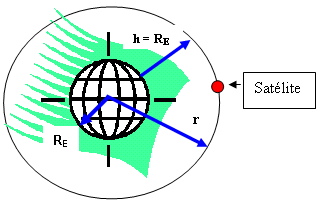
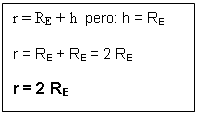
∑ FY = m a como el satélite se mantiene en orbita circular alrededor de la tierra. La fuerza de la gravedad hará las veces de fuerza centrípeta.
Ordenando la ecuación
m * g = m * a
De lo anterior se deduce que: 
Se cancela la masa m y r
Reemplazando r =2 RE
Multiplicamos por RE
Ordenando la ecuación
Pero: 
Reemplazando g (gravedad) en la ecuación, tenemos:
V = 5586,85 m/seg.
b) El periodo de su revolución (satelite)
Para calcular el periodo, sabemos que la rapidez promedio de una orbita circular del satélite es:
Despejamos el periodo
T = 238,79 minutos
c) La fuerza gravitacional que actúa sobre el?
Pero:  Reemplazando la gravedad en la ecuación anterior tenemos:
Reemplazando la gravedad en la ecuación anterior tenemos:
FR = 735 Newton
Leer más: http://www.monografias.com/trabajos38/movimiento-circular/movimiento-circular2.shtml#ixzz4hQzdNX8J
Comentarios
Publicar un comentario